Recently I was tasked with evaluating a tool used to predict violence. I initially created some code to plot ROC curves in SPSS for multiple classifiers, but then discovered that the ROC command did everything I wanted. Some recommend precision-recall curves in place of ROC curves, especially when the positive class is rare. This fit my situation (a few more than 100 positive cases in a dataset of 1/2 million) and it was pretty simple to adapt the code to return the precision. I will not go into the details of the curves (I am really a neophyte at this prediction stuff), but here are a few resources I found useful:
- ROC vs precision-and-recall curves: Cross validated Q/A
- Precision and recall: Wikipedia page
- The Relationship Between Precision-Recall and ROC Curves: Davis and Goadrich, 2006
The macro is named !Roc and it takes three parameters:
Class– the numeric classifier (where higher equals a greater probability of being predicted)Target– the outcome you are trying to predict. Positive cases need to equal 1 and negative cases 0Suf– this the the suffix on the variables returned. The procedure returns “Sens[Suf]”, “Spec[Suf]” and “Prec[Suf]” (which are the sensitivity, specificity, and precision respectively).
So here is a brief made up example using the macro to draw ROC and precision and recall curves (entire syntax including the macro can be found here). So first lets make some fake data and classifiers. Here Out is the target being predicted, and I have two classifiers, X and R. R is intentionally made to be basically random. The last two lines show an example of calling the macro.
SET SEED 10.
INPUT PROGRAM.
LOOP #i = 20 TO 70.
COMPUTE X = #i + RV.UNIFORM(-10,10).
COMPUTE R = RV.NORMAL(45,10).
COMPUTE Out = RV.BERNOULLI(#i/100).
END CASE.
END LOOP.
END FILE.
END INPUT PROGRAM.
DATASET NAME RocTest.
DATASET ACTIVATE RocTest.
EXECUTE.
!Roc Class = X Target = Out Suf = "_X".
!Roc Class = R Target = Out Suf = "_R".Now we can make an ROC curve plot with this information. Here I use inline TRANS statements to calculate 1 minus the specificity. I also use a blending trick in GPL to make the beginning of the lines connect at (0,0) and the end at (1,1).
*Now make a plot with both classifiers on it.
GGRAPH
/GRAPHDATASET NAME="graphdataset" VARIABLES=Spec_X Sens_X Spec_R Sens_R
/GRAPHSPEC SOURCE=INLINE.
BEGIN GPL
PAGE: begin(scale(770px,600px))
SOURCE: s=userSource(id("graphdataset"))
DATA: Spec_X=col(source(s), name("Spec_X"))
DATA: Sens_X=col(source(s), name("Sens_X"))
DATA: Spec_R=col(source(s), name("Spec_R"))
DATA: Sens_R=col(source(s), name("Sens_R"))
TRANS: o = eval(0)
TRANS: e = eval(1)
TRANS: SpecM_X = eval(1 - Spec_X)
TRANS: SpecM_R = eval(1 - Spec_R)
COORD: rect(dim(1,2), sameRatio())
GUIDE: axis(dim(1), label("1 - Specificity"), delta(0.1))
GUIDE: axis(dim(2), label("Sensitivity"), delta(0.1))
GUIDE: text.title(label("ROC Curve"))
SCALE: linear(dim(1), min(0), max(1))
SCALE: linear(dim(2), min(0), max(1))
ELEMENT: edge(position((o*o)+(e*e)), color(color.lightgrey))
ELEMENT: line(position(smooth.step.right((o*o)+(SpecM_R*Sens_R)+(e*e))), color("R"))
ELEMENT: line(position(smooth.step.right((o*o)+(SpecM_X*Sens_X)+(e*e))), color("X"))
PAGE: end()
END GPL.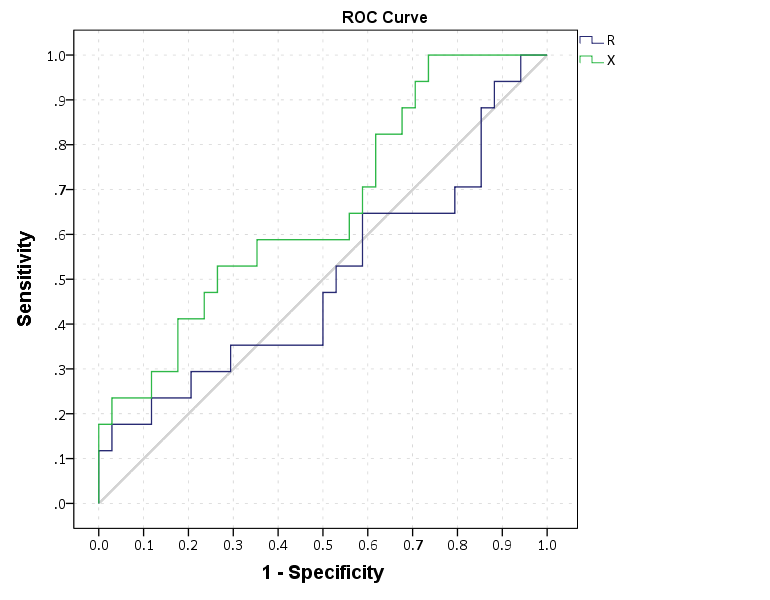
This just replicates the native SPSS ROC command though, and that command returns other useful information as well (such as the actual area under the curve). We can see though that my calculations of the curve are correct.
*Compare to SPSS's ROC command.
ROC R X BY Out (1)
/PLOT CURVE(REFERENCE)
/PRINT SE COORDINATES.
To make a precision-recall graph we need to use the path element and sort the data in a particular way. (SPSS’s line element works basically the opposite of the way we need it to produce the correct sawtooth pattern.) The blending trick does not work with this graph, but it is immaterial in interpreting the graph.
*Now make precision recall curves.
*To make these plots, need to reshape and sort correctly, so the path follows correctly.
VARSTOCASES
/MAKE Sens FROM Sens_R Sens_X
/MAKE Prec FROM Prec_R Prec_X
/MAKE Spec FROM Spec_R Spec_X
/INDEX Type.
VALUE LABELS Type
1 'R'
2 'X'.
SORT CASES BY Sens (A) Prec (D).
GGRAPH
/GRAPHDATASET NAME="graphdataset" VARIABLES=Sens Prec Type
/GRAPHSPEC SOURCE=INLINE.
BEGIN GPL
PAGE: begin(scale(770px,600px))
SOURCE: s=userSource(id("graphdataset"))
DATA: Sens=col(source(s), name("Sens"))
DATA: Prec=col(source(s), name("Prec"))
DATA: Type=col(source(s), name("Type"), unit.category())
COORD: rect(dim(1,2), sameRatio())
GUIDE: axis(dim(1), label("Recall"), delta(0.1))
GUIDE: axis(dim(2), label("Precision"), delta(0.1))
GUIDE: text.title(label("Precision-Recall Curve"))
SCALE: linear(dim(1), min(0), max(1))
SCALE: linear(dim(2), min(0), max(1))
ELEMENT: path(position(Sens*Prec), color(Type))
PAGE: end()
END GPL.
*The sawtooth is typical.
These curves both show that X is the clear winner. In my use application the ROC curves are basically superimposed, but there is more separation in the precision-recall graph. Being very generic, most of the action in the ROC curve is at the leftmost area of the graph (with only a few positive cases), but the PR curve is better at identifying how wide you have to cast the net to find the few positive cases. In a nut-shell, you have to be willing to live with many false positives to be able to predict just the few positive cases.
I would be interested to hear other analysts perspective. Predicting violence is a popular topic in criminology, with models of varying complexity. But what I’m finding so far in this particular evaluation is basically that there are set of low hanging fruit of chronic offenders that score high no matter how much you crunch the numbers (around 60% of the people who committed serious violence in a particular year in my sample), and then a set of individuals with basically no prior history (around 20% in my sample). So basically ad-hoc scores are doing about as well predicting violence as more complicated machine learning models (even machine learning models fit on the same data).


3 Comments